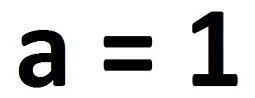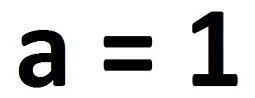Infinite Range of Golden Ratios
Infinite PHI – ∞ φ
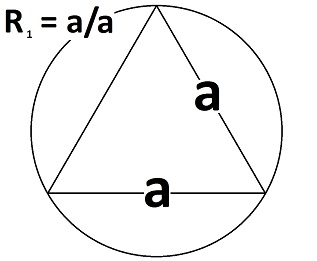
PHI series of numbers, 1st order: 1
Since this is a 1st order PHI, it has no further iterations. Once is all unity needs to authenticate itself.
It also has no relationship with any other value, so there is no need to approximate its solution by dividing some other number into unity!
Hence, all we get is...
X = 1
Subtracting 1 from both sides, we get...
A linear polynomial in one unknown: X − 1 = 0
PHI series of numbers, 2nd order:
| ' . "\n";
echo '' . "\n";
echo 'a' . "\n";
echo '' . "\n";
echo ' | ' . "\n";
echo ' | ' . "\n";
echo '' . "\n";
echo 'b' . "\n";
echo '' . "\n";
echo ' | ' . "\n";
echo ' |
|---|
' . "\n";
echo '| ' . "\n";
echo $diagonals[0][0] . "\n";
echo ' | ' . "\n";
echo '÷' . "\n";
echo ' | ' . "\n";
echo $diagonals[1][0] . "\n";
echo ' | ' . "\n";
echo '=' . "\n";
echo ' | ' . "\n";
echo 'NULL' . "\n";
echo ' |
| ' . "\n";
for ($i = 1; $i <= $print_limit; $i++)
{
echo $diagonals[0][$i] . "\n";
echo ' | ' . "\n";
echo '÷' . "\n";
echo ' | ' . "\n";
echo $diagonals[1][$i] . "\n";
echo ' | ' . "\n";
echo '=' . "\n";
echo ' | ' . "\n";
echo $diagonals[0][$i] / $diagonals[1][$i] . "\n";
echo ' |
| ' . "\n";
}
echo ' |
' . "\n\n";
echo '
' . "\n\n" . '
' . "\n\n";
$root1 = $diagonals[0][$print_limit] / $diagonals[1][$print_limit];
$root2 = $diagonals[1][$print_limit] / $diagonals[0][$print_limit];
echo '' . "\n\n";
echo 'After ' . $print_limit . ' iterations, it\'s pretty obvious that the approximation of the 2nd order of PHI accurate to eleven decimal places is... ' . "\n\n";
echo '' . $root1 . '' . "\n\n" . '
' . "\n\n";
echo 'And it\'s reciprocal is... ' . "\n\n";
echo '' . $root2 . '' . "\n\n" . '
' . "\n\n";
echo 'To be able to make a 2nd order polynomial in one unknown out of these two numbers will require that one of them is given a negative sign value...' . "\n\n";
echo '− ' . $root2 . '' . "\n\n" . '
' . "\n\n";
echo 'Now we can form this polynomial by multiplying these two values together. But first, we have to turn them into linear expressions in one unknown...' . "\n\n" . '
' . "\n\n";
echo 'X1 = ' . $root1 . '' . "\n\n" . '
' . "\n\n";
echo 'Subtract ' . $root1 . ' from both sides of the equal sign...' . "\n\n" . '
' . "\n\n";
echo 'X1 − ' . $root1 . ' = ' . $root1 . ' − ' . $root1 . '' . "\n\n" . '
' . "\n\n";
echo 'Yields... ' . "\n\n" . '
' . "\n\n";
echo '(X − ' . $root1 . ') = 0' . "\n\n" . '
' . "\n\n";
echo 'X2 = − ' . $root2 . '' . "\n\n" . '
' . "\n\n";
echo 'Add ' . $root2 . ' to both sides of the equal sign...' . "\n\n" . '
' . "\n\n";
echo 'X2 + ' . $root2 . ' = − ' . $root2 . ' + ' . $root2 . '' . "\n\n" . '
' . "\n\n";
echo 'Yields... ' . "\n\n" . '
' . "\n\n";
echo '(X + ' . $root2 . ') = 0' . "\n\n" . '
' . "\n\n";
echo 'Multiplying these two roots together... ' . "\n\n" . '
' . "\n\n";
echo '(X − ' . $root1 . ') × (X + ' . $root2 . ') = 0' . "\n\n" . '
' . "\n\n";
echo 'Yields... ' . "\n\n" . '
' . "\n\n";
echo 'X2 + ' . $root2 . 'X1 − ' . $root1 . 'X1 − ' . $root1 * $root2 . ' = 0' . "\n\n";
?>
Simplifying further, yields a quadratic polynomial in one unknown...
X2 − X1 − 1 = 0
PHI series of numbers, 3rd order:
| ' . "\n";
echo '' . "\n";
echo 'a' . "\n";
echo '' . "\n";
echo ' | ' . "\n";
echo '' . "\n";
echo 'b' . "\n";
echo '' . "\n";
echo ' | ' . "\n";
echo '' . "\n";
echo 'c' . "\n";
echo '' . "\n";
echo ' |
|---|
' . "\n";
echo '| ' . "\n";
echo $diagonals[0][0] . "\n";
echo ' | ' . "\n";
echo $diagonals[1][0] . "\n";
echo ' | ' . "\n";
echo $diagonals[2][0] . "\n";
echo ' |
' . "\n";
for ($i = 1; $i <= $print_limit; $i++)
{
echo '| ' . "\n";
echo $diagonals[0][$i] . "\n";
echo ' | ' . "\n";
echo $diagonals[1][$i] . "\n";
echo ' | ' . "\n";
echo $diagonals[2][$i] . "\n";
echo ' |
' . "\n";
}
?>
' . "\n\n";
echo 'After ' . $print_limit . ' iterations, the approximation of the three roots of the 2nd order of PHI accurate to eleven decimal places are... ' . "\n" . '
' . "\n";
echo 'X1 = a/c = ' . $diagonals[0][$print_limit] . ' ÷ ' . $diagonals[2][$print_limit] . ' = ' . $root1 . '' . "\n" . '
' . "\n";
echo 'X2 = b/a = ' . $diagonals[1][$print_limit] . ' ÷ ' . $diagonals[0][$print_limit] . ' = ' . $root2 . '' . "\n" . '
' . "\n";
echo 'X3 = c/b = ' . $diagonals[2][$print_limit] . ' ÷ ' . $diagonals[1][$print_limit] . ' = ' . $root3 . '' . "\n" . '
' . "\n";
echo 'To be able to make a 3rd order polynomial in one unknown out of these three numbers will require that one of them is given a negative sign value...' . "\n\n";
echo '− ' . $root2 . '' . "\n\n" . '
' . "\n\n";
echo 'Now we can form this polynomial by multiplying these three values together. But first, we have to turn them into linear expressions in one unknown...' . "\n\n" . '
' . "\n\n";
echo 'X1 = ' . $root1 . '' . "\n\n" . '
' . "\n\n";
echo 'Subtract ' . $root1 . ' from both sides of the equal sign...' . "\n\n" . '
' . "\n\n";
echo 'X1 − ' . $root1 . ' = ' . $root1 . ' − ' . $root1 . '' . "\n\n" . '
' . "\n\n";
echo 'Yields... ' . "\n\n" . '
' . "\n\n";
echo '(X − ' . $root1 . ') = 0' . "\n\n" . '
' . "\n\n";
echo 'X2 = − ' . $root2 . '' . "\n\n" . '
' . "\n\n";
echo 'Add ' . $root2 . ' to both sides of the equal sign...' . "\n\n" . '
' . "\n\n";
echo 'X2 + ' . $root2 . ' = − ' . $root2 . ' + ' . $root2 . '' . "\n\n" . '
' . "\n\n";
echo 'Yields... ' . "\n\n" . '
' . "\n\n";
echo '(X + ' . $root2 . ') = 0' . "\n\n" . '
' . "\n\n";
echo 'X3 = ' . $root3 . '' . "\n\n" . '
' . "\n\n";
echo 'Subtract ' . $root3 . ' from both sides of the equal sign...' . "\n\n" . '
' . "\n\n";
echo 'X3 − ' . $root3 . ' = ' . $root3 . ' − ' . $root3 . '' . "\n\n" . '
' . "\n\n";
echo 'Yields... ' . "\n\n" . '
' . "\n\n";
echo '(X − ' . $root3 . ') = 0' . "\n\n" . '
' . "\n\n";
echo 'Multiplying these three roots together... ' . "\n\n" . '
' . "\n\n";
echo '(X − ' . $root1 . ') × (X + ' . $root2 . ') × (X − ' . $root3 . ') = 0' . "\n\n" . '
' . "\n\n";
echo 'Yields... ' . "\n\n" . '
' . "\n\n";
echo 'X3 − ' . $root1 . 'X2 + ' . $root2 . 'X2 − ' . $root3 . 'X2 − ';
echo $root1 * $root2 . 'X1 + ' . $root1 * $root3 . 'X1 − ' . $root2 * $root3 . 'X1 + ' . $root1 * $root2 * $root3 . ' = 0';
?>
Simplifying further, yields a 3rd order polynomial in one unknown...
X3 ' . $coeff2 . 'X2 ' . $coeff1 . 'X1 + 1 = 0' . "\n" . '' . "\n\n";
?>
PHI series of numbers, 4th order:
| ' . "\n";
echo '' . "\n";
echo 'a' . "\n";
echo '' . "\n";
echo ' | ' . "\n";
echo '' . "\n";
echo 'b' . "\n";
echo '' . "\n";
echo ' | ' . "\n";
echo '' . "\n";
echo 'c' . "\n";
echo '' . "\n";
echo ' | ' . "\n";
echo '' . "\n";
echo 'd' . "\n";
echo '' . "\n";
echo ' |
|---|
' . "\n";
echo '| ' . "\n";
echo $diagonals[0][0] . "\n";
echo ' | ' . "\n";
echo $diagonals[1][0] . "\n";
echo ' | ' . "\n";
echo $diagonals[2][0] . "\n";
echo ' | ' . "\n";
echo $diagonals[3][0] . "\n";
echo ' |
' . "\n";
for ($i = 1; $i <= $print_limit; $i++)
{
echo '| ' . "\n";
echo $diagonals[0][$i] . "\n";
echo ' | ' . "\n";
echo $diagonals[1][$i] . "\n";
echo ' | ' . "\n";
echo $diagonals[2][$i] . "\n";
echo ' | ' . "\n";
echo $diagonals[3][$i] . "\n";
echo ' |
' . "\n";
}
?>
' . "\n\n";
echo 'After ' . $print_limit . ' iterations, the approximation of the four roots of the 4th order of PHI accurate to eleven decimal places are... ' . "\n" . '
' . "\n";
echo 'X1 = a/d = ' . $diagonals[0][$print_limit] . ' ÷ ' . $diagonals[3][$print_limit] . ' = ' . $root1 . '' . "\n" . '
' . "\n";
echo 'X2 = b/b = ' . $diagonals[1][$print_limit] . ' ÷ ' . $diagonals[1][$print_limit] . ' = ' . $root2 . '' . "\n" . '
' . "\n";
echo 'X3 = c/a = ' . $diagonals[2][$print_limit] . ' ÷ ' . $diagonals[0][$print_limit] . ' = ' . $root3 . '' . "\n" . '
' . "\n";
echo 'X4 = d/c = ' . $diagonals[3][$print_limit] . ' ÷ ' . $diagonals[2][$print_limit] . ' = ' . $root4 . '' . "\n" . '
' . "\n";
echo 'To be able to make a 4th order polynomial in one unknown out of these four numbers will require that two of them are given a negative sign value...' . "\n\n";
echo '− ' . $root2 . ' and' . "\n\n";
echo '− ' . $root4 . '' . "\n\n" . '
' . "\n\n";
echo 'Now we can form this polynomial by multiplying these four values together. But first, we have to turn them into linear expressions in one unknown...' . "\n\n" . '
' . "\n\n";
echo 'X1 = ' . $root1 . '' . "\n\n" . '
' . "\n\n";
echo 'Subtract ' . $root1 . ' from both sides of the equal sign...' . "\n\n" . '
' . "\n\n";
echo 'X1 − ' . $root1 . ' = ' . $root1 . ' − ' . $root1 . '' . "\n\n" . '
' . "\n\n";
echo 'Yields... ' . "\n\n" . '
' . "\n\n";
echo '(X − ' . $root1 . ') = 0' . "\n\n" . '
' . "\n\n";
echo 'X2 = − ' . $root2 . '' . "\n\n" . '
' . "\n\n";
echo 'Add ' . $root2 . ' to both sides of the equal sign...' . "\n\n" . '
' . "\n\n";
echo 'X2 + ' . $root2 . ' = − ' . $root2 . ' + ' . $root2 . '' . "\n\n" . '
' . "\n\n";
echo 'Yields... ' . "\n\n" . '
' . "\n\n";
echo '(X + ' . $root2 . ') = 0' . "\n\n" . '
' . "\n\n";
echo 'X3 = ' . $root3 . '' . "\n\n" . '
' . "\n\n";
echo 'Subtract ' . $root3 . ' from both sides of the equal sign...' . "\n\n" . '
' . "\n\n";
echo 'X3 − ' . $root3 . ' = ' . $root3 . ' − ' . $root3 . '' . "\n\n" . '
' . "\n\n";
echo 'Yields... ' . "\n\n" . '
' . "\n\n";
echo '(X − ' . $root3 . ') = 0' . "\n\n" . '
' . "\n\n";
echo 'X4 = − ' . $root4 . '' . "\n\n" . '
' . "\n\n";
echo 'Add ' . $root4 . ' to both sides of the equal sign...' . "\n\n" . '
' . "\n\n";
echo 'X4 + ' . $root4 . ' = − ' . $root4 . ' + ' . $root4 . '' . "\n\n" . '
' . "\n\n";
echo 'Yields... ' . "\n\n" . '
' . "\n\n";
echo '(X + ' . $root4 . ') = 0' . "\n\n" . '
' . "\n\n";
echo 'Multiplying these four roots together... ' . "\n\n" . '
' . "\n\n";
echo '(X − ' . $root1 . ') × (X + ' . $root2 . ') × (X − ' . $root3 . ') × (X + ' . $root4 . ') = 0' . "\n\n" . '
' . "\n\n";
echo 'Yields... ' . "\n\n" . '
' . "\n\n";
echo 'X4 − ' . $root1 . 'X3 + ' . $root2 . 'X3 − ' . $root3 . 'X3 + ' . $root4 . 'X3';
echo ' Ê' . "\n\n" . '
' . "\n\n";
echo 'Ä − ' . $root1 * $root2 . 'X2 + ' . $root1 * $root3 . 'X2 − ' . $root1 * $root4 . 'X2 ';
echo 'Ê' . "\n\n" . '
' . "\n\n";
echo 'Ä − ' . $root2 * $root3 . 'X2 + ' . $root2 * $root4 . 'X2 − ' . $root3 * $root4 . 'X2';
echo ' Ê' . "\n\n" . '
' . "\n\n";
echo 'Ä + ' . $root1 * $root2 * $root3 . 'X1 − ' . $root1 * $root2 * $root4 . 'X1 + ' . $root1 * $root3 * $root4;
echo 'X1 − ' . $root2 * $root3 * $root4 . 'X1 + ' . $root1 * $root2 * $root3 * $root4 . ' = 0' . "\n\n";
?>
Simplifying further, yields a 4th order polynomial in one unknown...
X4 ' . $coeff3 . 'X3 ' . $coeff2. 'X2 + ' . $coeff1 . 'X1 + 1 = 0' . "\n" . '' . "\n\n";
?>
The Expanded Euclidean Algorithm arises from the Infinite Range of Golden Ratios...